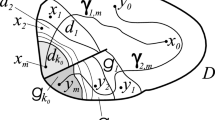
We present a canonical representation of prime ends in regular domains and, on this basis, study the boundary behavior of the so-called lower Q-homeomorphisms obtained as a natural generalization of quasiconformal mappings. We establish a series of effective conditions imposed on a function Q(x) for the homeomorphic extension of given mappings with respect to prime ends in domains with regular boundaries. The developed theory is applicable, in particular, to mappings of the Orlicz–Sobolev classes and also to finitely bi-Lipschitz mappings, which can be regarded as a significant generalization of the well-known classes of isometric and quasiisometric mappings.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. Gutlyanskii, V. Ryazanov, U. Srebro, and E. Yakubov, The Beltrami Equations: A Geometric Approach, Springer, New York (2012).
F. W. Gehring, “Rings and quasiconformal mappings in space,” Trans. Amer. Math. Soc., 103, No. 3, 353–393 (1962).
G. M. Goluzin, Geometric Theory of Functions of Complex Variable [in Russian], Nauka, Moscow (1966).
A. A. Ignat’ev and V. I. Ryazanov, “Finite mean oscillation in the mapping theory,” Ukr. Mat. Vestn., 2, No. 3, 395–417 (2005).
D. A. Kovtonyuk and V. I. Ryazanov, “On the theory of boundaries of space domains,” Tr. Inst. Prikl. Mat. Mekh., Nats. Akad. Nauk Ukr., 13, 110–120 (2006).
D. A. Kovtonyuk and V. I. Ryazanov, “On the theory of lower Q-homeomorphisms,” Ukr. Mat. Vestn., 5, No. 2, 157–181 (2008).
D. Kovtonyuk and V. Ryazanov, “On the boundary behavior of generalized quasi-isometries,” J. Anal. Math., 115, 103–119 (2011).
D. A. Kovtonyuk, V. I. Ryazanov, R. R. Salimov, and E. A. Sevost’yanov, “On the theory of the Orlicz–Sobolev classes,” Algebra Analiz, 25, No. 6, 49–101 (2013).
D. A. Kovtonyuk, R. R. Salimov, and E. A. Sevost’yanov, On the Theory of Mappings for the Sobolev and Orlicz–Sobolev Classes [in Russian], Naukova Dumka, Kiev (2013).
E. F. Collingwood and A. J. Lohwater, The Theory of Cluster Sets, Cambridge Univ. Press, Cambridge (1966).
O. Martio, V. Ryazanov, U. Srebro, and E. Yakubov, Moduli in Modern Mapping Theory, Springer, New York (2009).
R. Näkki, “Prime ends and quasiconformal mappings,” J. Anal. Math., 35, 13–40 (1979).
M. Ohtsuka, Extremal Length and Precise Functions, Gakkotosho Co., Tokyo (2003).
T. Rado and P. V. Reichelderfer, Continuous Transformations in Analysis, Springer, Berlin (1955).
S. Rickman, Quasiregular Mappings, Springer, Berlin (1993).
V. I. Ryazanov and R. R. Salimov, “Weakly plane spaces and boundaries in the mapping theory,” Ukr. Mat. Vestn., 4, No. 2, 199–234 (2007).
V. I. Ryazanov and E. A. Sevost’yanov, “Equicontinuous classes of ring Q-homeomorphisms,” Sib. Mat. Zh., 48, No. 6, 1361–1376 (2007).
V. Ryazanov, U. Srebro, and E. Yakubov, “On integral conditions in the mapping theory,” Ukr. Math. Bull., 7, No. 1, 73–87 (2010).
S. Saks, Theory of the Integral, Państwowe Wydawnictwo Naukowe, Warsaw (1937).
V. A. Shlyk, “On the equality of p-capacity and p-module,” Sib. Mat. Zh., 34, No. 6, 216–221 (1993).
A.Vasil’ev, Moduli of Families of Curves for Conformal and Quasiconformal Mappings, Springer, Berlin (2002).
J. Väisälä, Lectures on n-Dimensional Quasiconformal Mappings, Springer, Berlin (1971).
M. Vuorinen, Conformal Geometry and Quasiregular Mappings, Springer, Berlin (1988).
G. T. Whyburn, Analytic Topology, American Mathematical Society, Providence, RI (1942).
R. L. Wilder, Topology of Manifolds, American Mathematical Society, New York (1949).
W. P. Ziemer, “Extremal length and conformal capacity,” Trans. Amer. Math. Soc., 126, No. 3, 460–473 (1967).
Author information
Authors and Affiliations
Additional information
Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 67, No. 4, pp. 467–479, April, 2015.
Rights and permissions
About this article
Cite this article
Kovtonyuk, D.A., Ryazanov, V.I. On the Theory of Prime Ends for Space Mappings. Ukr Math J 67, 528–541 (2015). https://doi.org/10.1007/s11253-015-1098-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-015-1098-9