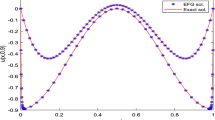
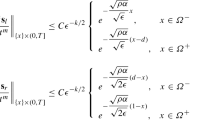
The accuracy and convergence of the numerical solutions of a stationary one-dimensional linear convection-diffusion-reaction equation (with Dirichlet boundary conditions) by the Petrov–Galerkin finiteelement method with piecewise-linear basis functions and piecewise-quadratic weighting functions are analyzed and the accuracy estimates of the method are obtained in certain norms depending on the choice of the collection of stabilization parameters of weight functions.
Similar content being viewed by others
References
B. A. Finlayson, Numerical Methods for Problems with Moving Fronts, Ravenna Park Publishing, Seattle (1992).
V. S. Deineka, I. V. Sergienko, and V. V. Skopetskii, Mathematical Models and Methods of Analysis in Problems with Discontinuous Solutions [in Russian], Naukova Dumka, Kiev (1995).
H.-G. Roos, M. Stynes, and L. Tobiska, Robust Numerical Methods for Singularly Perturbed Differential Equations, Springer, Berlin (2008).
A. N. Tikhonov and A. A. Samarskii, Equations of Mathematical Physics [in Russian], Nauka, Moscow (1972).
A. A. Samarskii and P. N. Vabishchevich, Numerical Methods for the Solution of Convection-Diffusion Equations [in Russian], Nauka, Moscow (2009).
C. Grossmann, H.-G. Roos, and M. Stynes, Numerical Treatment of Partial Differential Equations, Springer, Berlin (2007).
T. P. Fries and H. G. Matthies, A Review of Petrov–Galerkin Stabilization Approaches and an Extension to Mesh-Free Methods, Technische Universität Braunschweig, Informatikbericht 2004-1, Brunswick (2004).
T. J. R. Hughes, G. Scovazzi, and T. E. Tezduyar, “Stabilized methods for compressible flows,” J. Sci. Comput., 43, 343–368 (2010).
V. John and E. Schmeyer, “Finite-element methods for time-dependent convection-diffusion-reaction equations with small diffusion,” Comput. Meth. Appl. Mech. Eng., 198, 475–494 (2008).
S. V. Sirik, “Exactness and stability of the Petrov–Galerkin method in the integration of the stationary convection-diffusion equation,” Kibernet. Sistem. Anal., 50, No. 2, 32–143 (2014).
D. F. Griffiths and J. Lorenz, “An analysis of the Petrov–Galerkin finite element method,” Comput. Meth. Appl. Mech. Eng., 14, 39–64 (1978).
K. W. Morton, “Finite element methods for nonself-adjoint problems,” in: P. R. Turner (editor), Proc. of the SERC Summer School (Lancaster, 1981), 965, Springer, Berlin (1982), pp. 113–148.
D. F. Griffiths, “Discretized eigenvalue problems, LBB constants and stabilization,” Numer. Anal., Longman, Edinburgh, 57–75 (1996).
D. Gilbarg and N. S. Trudinger, Elliptic Partial Differential Equations of Second Order, Springer, Berlin (1983).
S. Agmon, Lectures on Elliptic Boundary Value Problems, Van Nostrand, Princeton (1965).
A. R. Mitchell and R. Wait, The Finite Element Method in Partial Differential Equations, Wiley, New York (1977).
K. Rektorys, Variational Methods in Mathematics, Science and Engineering, Reidel, Dordrecht (1980).
O. A. Ladyzhenskaya, Boundary-Value Problems of Mathematical Physics [in Russian], Nauka, Moscow (1973).
I. Babuška and A. K. Aziz, “Survey lectures on the mathematical foundations of the finite element method,” in: A. K. Aziz (editor), The Mathematical Foundations of the Finite Element Method with Applications to Partial Differential Equations, Academic Press, New York (1972), pp. 2–363.
N. N. Sal’nikov, S. V. Sirik, and I. A. Tereshchenko, “On the construction of a finite-dimensional mathematical model of the convection-diffusion process with the use of the Petrov–Galerkin method,” Probl. Upravl. Inform., No. 3, 94–109 (2010).
S. V. Sirik, N. N. Sal’nikov, and V. K. Beloshapkin, “The choice of weight functions in the Petrov–Galerkin method for the integration of linear one-dimensional convection-diffusion equations,” Upravl. Sist. Mash., No. 1, 38–47 (2014).
J. Xu and L. Zikatanov, “Some observations on the Babuška and Brezzi theories,” Numer. Math., 94, 195–202 (2003).
R. A. Horn and C. R. Johnson, Matrix Analysis, Cambridge Univ. Press, Cambridge (1986).
K. Dekker and J. G. Verwer, Stability of Runge–Kutta Methods for Stiff Nonlinear Differential Equations, North-Holland, Amsterdam (1984).
C. A. Desoer and H. Haneda, “The measure of a matrix as a tool to analyze computer algorithms for circuit analysis,” IEEE Trans. Circ. Theory, 19, No. 5, 480–486 (1972).
A. A. Samarskii and A. V. Gulin, Numerical Methods of Mathematical Physics [in Russian], Nauch. Mir, Moscow (2003).
S. Noschese, L. Pasquini, and L. Reichel, “Tridiagonal Toeplitz matrices: properties and novel applications,” Numer. Linear Algebra Appl., 20, No. 2, 302–326 (2013).
S. C. Brenner and R. Scott, The Mathematical Theory of Finite Element Methods, Springer, Berlin (2007).
V. C. L. Hutson and J. S. Pym, Application of Functional Analysis and Operator Theory, Academic Press, London (1983).
K.-J. Bathe, D. Hendriana, F. Brezzi, and G. Sangalli, “Inf-sup testing of upwind methods,” Int. J. Numer. Meth. Eng., 48, 745–760 (2000).
G. Sangalli, “Numerical evaluation of finite element methods in convection-diffusion problems,” Calcolo, 37, 233–251 (2000).
G. Sangalli, “Numerical evaluation of FEM with application to the 1-D advection-diffusion problem,” Math. Models Meth. Appl. Sci., 12, No. 2, 205–228. (2002).
A. Buffa, C. de Falco, and G. Sangalli, “Isogeometric analysis: stable elements for the 2D Stokes equation,” Int. J. Numer. Meth. Fluids, 65, 1407–1422 (2011).
E. Abramov, H. Kvasnytsya, and H. Shynkarenko, “Partially quadratic and cubic approximations of h -adaptive FEM for onedimensional boundary-value problems,” Visn. Lviv. Univ., Ser. Prykl. Mat. Inform., Issue 17, 47–61 (2011).
V. M. Trushevs’kyi and H. Shynkarenko, “Parallel approximation of elliptic boundary-value problems with artificial neuroboundary with radial basis functions,” Visn. Lviv. Univ., Ser. Prykl. Mat. Inform., Issue 22, 108–117 (2014).
A. Berman and R. J. Plemmons, Nonnegative Matrices in the Mathematical Sciences, SIAM, Philadelphia (1994).
C. A. J. Fletcher, Computational Galerkin Methods, Springer, New York (1984).
Author information
Authors and Affiliations
Additional information
Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 67, No. 7, pp. 937–961, July, 2014.
Rights and permissions
About this article
Cite this article
Sirik, S.V. Estimation of the Accuracy of Finite-Element Petrov–Galerkin Method in Integrating the One-Dimensional Stationary Convection-Diffusion-Reaction Equation. Ukr Math J 67, 1062–1090 (2015). https://doi.org/10.1007/s11253-015-1135-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-015-1135-8