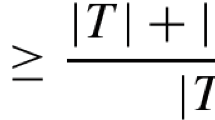Let G be a group and let Z(G) be the center of G. The commuting graph of the group G is an undirected graph Γ(G) with the vertex set G \ Z(G) such that two vertices x, y are adjacent if and only if xy = yx. We study the commuting graphs of permutational wreath products H
G, where G is a transitive permutation group acting on X (the top group of the wreath product) and (H, Y) is an Abelian permutation group acting on Y.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. Iranmanesh and A. Jafarzadeh, “On the commuting graph associated with the symmetric and alternating groups,” J. Algebra Appl., 7, No. 1, 129–146 (2008).
M. Giudici and C. Parker, “There is no upper bound for the diameter of the commuting graph of a finite group,” arXiv 2012 (http://arxiv.org/abs/1210.0348v1).
S. Akbari, A. Mohammadian, H. Radjavi, and P. Raja, “On the diameters of commuting graphs,” Linear Algebra Appl., 418, No. 1, 161–176 (2006).
A. R. Moghaddamfar, “About noncommuting graphs,” Sib. Mat. Zh., 47, No. 5, 911–914 (2006).
A. Abdollahi, S. Akbari, H. Dorbidi, and H. Shahverdi, “Commutativity pattern of finite non-Abelian p-groups determines their orders,” Comm. Algebra, 41, No. 2, 451–461 (2013).
G. L. Morgan and C. W. Parker, “The diameter of the commuting graph of a finite group with trivial centre,” arXiv 2013 (http://arxiv.org/abs/1301.2341v1).
M. Guidici and A. Pope, “On bounding the diameter of the commuting graph of a group,” arXiv 2012 (http://arxiv.org/abs/1206.3731).
L. Kaloujnine, “La structure des p-groupes de Sylow des groupes symetriques finis,” Ann. Sci. l’Ecole Norm. Super., 65, 239–276 (1948).
A. S. Oliynyk and V. I. Sushchanskii, “The groups of ZC-automaton transformations,” Sib. Mat. Zh., 51, No. 5, 879–891 (2010).
P. M. Neumann, “On the structure of standard wreath products of groups,” Math. Zeitschr., 84, 343–373 (1964).
I. M. Isaacs, Finite Group Theory [Graduate Studies in Mathematics, Vol. 92], AMS, Providence, RI (2008).
Yu. Yu. Leshchenko and L. V. Zoria, “On diameters estimations of the commuting graphs of Sylow p-subgroups of the symmetric groups,” Carpat. Math. Publ., 5, No. 1, 70–78 (2013).
The GAP Group, GAP—Groups, Algorithms, and Programming, Version 4.6.3 (2013) (http://www.gap-system.org).
V. I. Sushchansky and V. S. Sikora, Operations on the Permutation Groups [in Ukrainian], Chernivtsi, Ruta (2003).
A. J. Slupik and V. I. Sushchansky, “Minimal generating sets and Cayley graphs of Sylow p-subgroups of finite symmetric groups,” Algebra Discr. Math., 4, 167–184 (2009).
A. J. Weir, “Sylow p-subgroups of the classical groups over finite fields with characteristic prime to p,” Proc. Amer. Math. Soc., 6, No. 4, 529–533 (1955).
Author information
Authors and Affiliations
Additional information
Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 66, No. 5, pp. 656–665, May, 2014.
Rights and permissions
About this article
Cite this article
Leshchenko, Y.Y. On the Diameters of Commuting Graphs of Permutational Wreath Products. Ukr Math J 66, 732–742 (2014). https://doi.org/10.1007/s11253-014-0968-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-014-0968-x