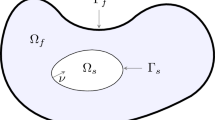
We study the dynamics of a coupled system formed by the 3D Navier–Stokes equations linearized near a certain Poiseuille-type flow in an (unbounded) domain and a classical (possibly nonlinear) equation for transverse displacements of an elastic plate in a flexible flat part of the boundary. We first show that this problem generates an evolution semigroup S t in an appropriate phase space. Then, under some conditions imposed on the underlying (Poiseuille-type) flow, we prove the existence of a compact finite-dimensional global attractor for this semigroup and also show that S t is an exponentially stable C 0 -semigroup of linear operators in the completely linear case. Since we do not assume any kind of mechanical damping in the plate component, this means that the dissipation of energy in the flow of fluid caused by viscosity is sufficient to stabilize the system.
Similar content being viewed by others
References
G. Avalos, “The strong stability and instability of a fluid-structure semigroup,” Appl. Math. Optimiz., 55, 163–184 (2007).
G. Avalos and R. Triggiani, “Semigroup well-posedness in the energy space of a parabolic hyperbolic coupled Stokes–Lamé PDE system of fluid-structure interaction,” Discrete Contin. Dynam. Syst., Ser. S, 2, 417–447 (2009).
A.V. Babin and M. I. Vishik, Attractors of Evolution Equations, North-Holland, Amsterdam (1992).
V. Barbu, Z. Grujić, I. Lasiecka, and A. Tuffaha, “Existence of the energy-level weak solutions for a nonlinear fluid-structure interaction model,” Fluids and Waves. Contemp. Math., 440, 55–82 (2007).
A. Chambolle, B. Desjardins, M. Esteban, and C. Grandmont, “Existence of weak solutions for the unsteady interaction of a viscous fluid with an elastic plate,” J. Math. Fluid and Mech., 7, 368–404 (2005).
A. J. Chorin and J. E. Marsden, A Mathematical Introduction to Fluid Mechanics, 3rd ed, Springer, New York (1993).
I. Chueshov, Introduction to the Theory of Infinite-Dimensional Dissipative Systems, Acta, Kharkov (2002); http://www.emis.de/monographs/Chueshov.
I. Chueshov, “A global attractor for a fluid-plate interaction model accounting only for longitudinal deformations of the plate,” Math. Meth. Appl. Sci., 34, 1801–1812 (2011).
I. Chueshov and S. Kolbasin, “Long-time dynamics in plate models with strong nonlinear damping,” Commun. Pure Appl. Anal., 11, 659–674 (2012).
I. Chueshov and I. Lasiecka, “Long-time behavior of second-order evolution equations with nonlinear damping,” Mem. AMS, 195, No. 912 (2008).
I. Chueshov and I. Lasiecka, Von Karman Evolution Equations, Springer, New York (2010).
I. Chueshov and I. Lasiecka, Well-Posedness and Long-Time Behavior in Nonlinear Dissipative Hyperbolic-Like Evolutions with Critical Exponents, Preprint ArXiv, 1204.5864v1.
I. Chueshov, I. Lasiecka, and J. Webster, “Evolution semigroups in supersonic flow-plate interactions,” J. Different. Equat., 254, 1741–1773 (2013).
I. Chueshov and I. Ryzhkova, “A global attractor for a fluid–plate interaction model,” Commun. Pure Appl. Anal., 12, 1635–1656 (2013).
I. Chueshov and I. Ryzhkova, “Unsteady interaction of a viscous fluid with an elastic shell modeled by full von Karman equations,” J. Different. Equat., 254, 1833–1862 (2013).
I. Chueshov and I. Ryzhkova, “Well-posedness and long time behavior for a class of fluid-plate interaction models,” IFIP Adv. Inform. Commun. Technology, Springer, Berlin (2013), Vol. 391, pp. 328–337.
D. Coutand and S. Shkoller, “Motion of an elastic solid inside an incompressible viscous fluid,” Arch. Ration. Mech. Anal., 176, 25–102 (2005).
G. Galdi, An Introduction to the Mathematical Theory of the Navier–Stokes Equations. Steady-State Problems, 2nd ed., Springer, New York (2011).
Q. Du, M. D. Gunzburger, L. S. Hou, and J. Lee, “Analysis of a linear fluid–structure interaction problem,” Discrete Contin. Dynam. Syst., 9, 633–650 (2003).
C. Grandmont, “Existence of weak solutions for the unsteady interaction of a viscous fluid with an elastic plate,” SIAM J. Math. Anal., 40, 716–737 (2008).
M. Grobbelaar-Van Dalsen, “A new approach to the stabilization of a fluid–structure interaction model,” Appl. Anal., 88, 1053–1065 (2009).
M. Grobbelaar-Van Dalsen, “Strong stability for a fluid–structure model,” Math. Meth. Appl. Sci., 32, 1452–1466 (2009).
M. Guidorzi, M. Padula, and P. I. Plotnikov, “Hopf solutions to a fluid–elastic interaction model,” M3AS, 18, 215–269 (2008).
N. Kopachevskii and Yu. Pashkova, “Small oscillations of a viscous fluid in a vessel bounded by an elastic membrane,” Rus. J. Math. Phys., 5, No. 4, 459–472 (1998).
O. Ladyzhenskaya, Mathematical Theory of Viscous Incompressible Flow, Gordon & Breach, New York (1969).
O. Ladyzhenskaya and V. Solonnikov, “Some problems of vector analysis and generalized formulations of boundary-value problems for the Navier–Stokes equations,” Zap. LOMI, 59, 81–116 (1976); English translation: J. Soviet Math., 10, 257–286 (1978).
J.-L. Lions and E. Magenes, Problémes aux Limites non Homogénes et Applications, Dunod, Paris (1968), Vol. 1.
J.-L. Lion, Quelques Methodes de Resolution des Problémes aux Limites Non Lineaire, Dunod, Paris (1969).
B. S. Massey and J. Ward-Smith, Mechanics of Fluids, 8th ed., Taylor & Francis, New York (2006).
A. Osses and J. Puel, “Approximate controllability for a linear model of fluid structure interaction,” ESIAM: Contr., Optimiz. and Calc. Variat., 4, 497–513 (1999).
G. Raugel, “Global attractors in partial differential equations,” Handbook Dynam. Syst., Elsevier Sci., Amsterdam (2002), Vol. 2, pp. 885–992.
J. Simon, “Compact sets in the space L p(0, T; B),” Ann. Mat. Pura Appl. Ser. 4, 148, 65–96 (1987).
R. Temam, Infinite-Dimensional Dynamical Systems in Mechanics and Physics, Springer, New York (1988).
R. Temam, Navier–Stokes Equations: Theory and Numerical Analysis, Reprint of the 1984 ed., AMS Chelsea Publ., Providence, RI (2001).
H. Triebel, Interpolation Theory, Functional Spaces, and Differential Operators, North-Holland, Amsterdam (1978).
Author information
Authors and Affiliations
Additional information
Published in Ukrains’kyi Matematychnyi Zhurnal, Vol. 65, No. 1, pp. 143–160, January, 2013.
Rights and permissions
About this article
Cite this article
Chueshov, I., Ryzhkova, I. On the interaction of an elasticwall with a poiseuille-type flow. Ukr Math J 65, 158–177 (2013). https://doi.org/10.1007/s11253-013-0771-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-013-0771-0