Skip to main content
SpringerLink
Log in

Vibrating Systems with Rigid Light-Weight Inclusions: Asymptotics of the Spectrum and Eigenspaces

  • Published:
Ukrainian Mathematical Journal Aims and scope

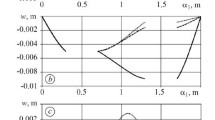
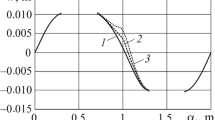
We study the asymptotic behavior of eigenvalues and eigenfunctions of a singularly perturbed boundaryvalue problem for a second-order elliptic operator. The problem simulates natural vibrations of an elastic system with finitely many light-weight inclusions of any shape. The leading terms of the asymptotic representations of eigenelements are constructed with regard for their multiplicities. The justification of the asymptotic formulas is based on the uniform resolvent convergence of a certain family of unbounded self-adjoint operators.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. A. Marchenko and E. Ya. Khruslov, Boundary-Value Problems in Domains with Fine-Grained Boundaries [in Russian], Naukova Dumka, Kiev (1974).

    Google Scholar 

  2. E. Sanchez-Palencia, Non-Homogeneous Media and Vibration Theory, Springer, New York (1980).

    MATH  Google Scholar 

  3. J. Sanchez-Hubert and E. Sanchez-Palencia, Vibration and Coupling of Continuous Systems, Springer, Berlin (1989).

    Book  MATH  Google Scholar 

  4. O. A. Oleinik, G. A. Iosif’yan, and A. S. Shamaev, Mathematical Problems of the Theory of Strongly Inhomogeneous Elastic Media [in Russian], Moscow University, Moscow (1990).

    Google Scholar 

  5. V. V. Zhikov, S. M. Kozlov, and O. A. Oleinik, Averaging of Differential Operators [in Russian], Fizmatgiz, Moscow (1993).

    Google Scholar 

  6. V. A. Marchenko and E. Ya. Khruslov, Averaged Models of Microinhomogeneous Media [in Russian], Naukova Dumka, Kiev (2005).

    Google Scholar 

  7. A. L. Pyatnitskii, G. A. Chechkin, and A. Shamaev, Averaging. Methods and Applications [in Russian], Tamara Rozhkovskaya, Novosibirsk (2007).

    Google Scholar 

  8. G. V. Sandrakov, “Averaging of the system of equations of the theory of elasticity with contrasting coefficients,” Mat. Sb., 190, No. 12, 37–92 (1999).

    Article  MathSciNet  Google Scholar 

  9. V. V. Zhikov, “On spectrum gaps of some divergent elliptic operators with periodic coefficients,” Alg. Anal., 16, Issue 5, 733–790 (2004).

    Google Scholar 

  10. A. Bourgeat, G. A. Chechkin, and A. L. Piatnitski, “Singular double porosity model,” Appl. Anal., 82, No. 2, 103–116 (2003).

    Article  MathSciNet  MATH  Google Scholar 

  11. G. Geymonat, M. Lobo-Hidalgo, E. Sanchez-Palencia, and G. F. Roach, “Spectral properties of certain stiff problems in elasticity and acoustics,” Math. Meth. Appl. Sci., 4, 291–306 (1982).

    Article  MATH  Google Scholar 

  12. M. Lobo, S. A. Nazarov, and E. Pérez, “Eigen-oscillations of contrasting non-homogeneous elastic bodies: asymptotic and uniform estimates for eigenvalues,” J. Appl. Math., 1–40 (2005).

  13. D. Gómez, M. Lobo, S. A. Nazarov, and E. Pérez, “Asymptotics for the spectrum of the Wentzell problem with a small parameter and other related stiff problems,” J. Math. Pures Appl., 86, 369–402 (2006).

    MathSciNet  MATH  Google Scholar 

  14. Yu. Golovaty and N. Babych, “On WKB asymptotic expansions of high frequency vibrations in stiff problems,” in: Proc. of Equadiff’ 99: Internat. Conf. on Differential Equations, World Scientific, Singapore (1999), pp. 103–105.

    Google Scholar 

  15. Yu. D. Golovatyi, “Spectral properties of vibrating systems with added masses: the effect of local vibrations,” Tr. Mosk. Mat. Obshch., 54, 29–72 (1992).

    Google Scholar 

  16. G. A. Chechkin, “Asymptotic decompositions of eigenvalues and eigenfunctions of the elliptic operator in domains with large numbers of ‘light’ concentrated masses closely located on the boundary. Two-dimensional case,” Izv. Ros. Akad. Nauk, Ser. Mat., 69, No. 4, 161–204 (2005).

    MathSciNet  Google Scholar 

  17. V. Rybalko, “Vibrations of elastic systems with a large number of tiny heavy inclusions,” Asymp. Anal., 32, 27–62 (2002).

    MathSciNet  MATH  Google Scholar 

  18. G. A. Chechkin and T. A. Mel’nyk, “Asymptotics of eigenelements to spectral problem in thick cascade junction with concentrated masses,” Appl. Anal., 1–41 (2011) (doi: 10.1080/00036811.2011.602634).

    Google Scholar 

  19. M. Lobo and E. Pérez, “Local problems for vibrating systems with concentrated masses: a review,” C. R. Mecanique, 331, 303–317 (2003).

    Article  MATH  Google Scholar 

  20. Yu. D. Golovaty, D. Gomez, M. Lobo, and E. Pérez, “Asymptotics for the eigenelements of vibrating membranes with very heavy thin inclusions,” C. R. Mecanique, 330(11), 777–782 (2002).

    Article  MATH  Google Scholar 

  21. Yu. D. Golovaty, D. Gomez, M. Lobo, and E. Pérez, “On vibrating membranes with very heavy thin inclusions,” Math. Models Meth. Appl. Sci., 14, No. 7, 987–1034 (2004).

    Article  MATH  Google Scholar 

  22. T. A. Mel’nik and S. A. Nazarov, “Asymptotic structure of the spectrum in the problem of harmonic vibrations of a hub with heavy spokes,” Dokl. Ros. Akad. Nauk, 333, No. 1, 13–15 (1993).

    Google Scholar 

  23. T. A. Mel’nik and S. A. Nazarov, “Asymptotic analysis of the Neumann problem for the joint of a body with heavy rods,” Alg. Anal., 12, No. 2, 188–238 (2000).

    MathSciNet  Google Scholar 

  24. Yu. Golovaty and N. Babych, “Asymptotic analysis of vibrating system containing stiff-heavy and flexible-light parts,” Nonlin. Boundary-Value Probl., 18, 194–207 (2008).

    MathSciNet  MATH  Google Scholar 

  25. Yu. D. Golovaty and N. Babych, “Low and high frequency approximations to eigenvibrations in a medium with double contrasts,” J. Comput. Appl. Math., 234, 1860–1867 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  26. R. Showalter, Hilbert Space Methods for Partial Differential Equations, Electron. J. Different. Equat., Monograph 01 (1994).

  27. Inverse Problems for Partial Differential Equations, 127, Springer, Berlin (1998).

  28. J. Sylvester and G. Uhlmann, “The Dirichlet to Neumann map and its applications,” in: Inverse Problems in Partial Differential Equations (1990), pp. 101–139.

  29. G. C. Hsiao and W. L. Wendland, Boundary Integral Equations, Springer, Berlin (2008).

    Book  MATH  Google Scholar 

  30. M. Reed and B. Simon, Methods of Modern Mathematical Physics. Vol. 1. Functional Analysis, Academic Press, New York (1972).

    Google Scholar 

  31. M. I. Vishik and A. A. Lyusternik, “Regular degeneration and boundary layer for linear differential equations with small parameter,” Usp. Mat. Nauk, 12, Issue 5, 3–122 (1957).

    MathSciNet  MATH  Google Scholar 

  32. V. F. Lazutkin, “Quasiclassical asymptotics of eigenfunctions,” in: VINITI Series in Contemporary Problems of Mathematics (Fundamental Trends) [in Russian], 34, VINITI, Moscow (1988), pp. 135–174.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Franko Lviv National University, Lviv, Ukraine

    Yu. D. Holovatyi & V. M. Hut

Authors
  1. Yu. D. Holovatyi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. M. Hut
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 64, No. 10, pp. 1314–1329, October, 2012.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Holovatyi, Y.D., Hut, V.M. Vibrating Systems with Rigid Light-Weight Inclusions: Asymptotics of the Spectrum and Eigenspaces. Ukr Math J 64, 1495–1513 (2013). https://doi.org/10.1007/s11253-013-0731-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11253-013-0731-8

Keywords

Search

Navigation