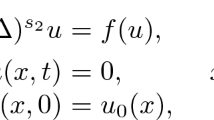Skip to main content
SpringerLink
Log in

On the behavior of solutions of the Cauchy problem for a degenerate parabolic equation with source in the case where the initial function slowly vanishes

  • Published:
Ukrainian Mathematical Journal Aims and scope

We study the Cauchy problem for a degenerate parabolic equation with source and inhomogeneous density of the form

$$ {u_t}=\mathrm{div}\left( {\rho (x){u^{m-1 }}{{{\left| {Du} \right|}}^{{\lambda -1}}}Du} \right)+{u^p} $$

in the case where the initial function slowly vanishes as |x| → ∞: We establish conditions for the existence and nonexistence of a global (in time) solution. These conditions strongly depend on the behavior of the initial data as |x| → ∞: In the case of global solvability, we establish a sharp estimate of the solution for large times.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Fujita, “On the blowing up of solutions to the Cauchy problem for u t = ∆u + u 1 + α,” J. Fac. Sci. Univ. Tokyo, Sec. I, 13, 109–124 (1966).

    MATH  Google Scholar 

  2. A. A. Samarskii, V. A. Galaktionov, S. P. Kurdyumov, and A. P. Mikhailov, “On unbounded solutions of the Cauchy problem for the parabolic equation u t = ∇(u σ∇u)u + u β;” Dokl. Akad. Nauk SSSR, 252, No. 6, 1362–1364 (1980).

    MathSciNet  Google Scholar 

  3. A. A. Samarskii, V. A. Galaktionov, S. P. Kurdyumov, and A. P. Mikhailov, Modes with Peaking in the Problems for Quasilinear Parabolic Equations [in Russian], Nauka, Moscow (1987).

    Google Scholar 

  4. D. Andreucci and E. Di Benedetto, “On the Cauchy problem and initial traces for a class of evolution equations with strongly nonlinear sources equations,” Ann. Sci. Norm. Super. Pisa, 18, 363–441 (1991).

    MATH  Google Scholar 

  5. V. A. Galaktionov, “On the conditions of absence of global solutions for a class of quasilinear parabolic equations,” Zh. Vychisl. Mat. Mat. Fiz., 22, No. 2, 322–338 (1982).

    MathSciNet  MATH  Google Scholar 

  6. V. A. Galaktionov and H. A. Levine, “A general approach to critical Fujita exponents and systems,” Nonlin. Anal., 34, 1005–1027 (1998).

    Article  MathSciNet  MATH  Google Scholar 

  7. D. Andreucci and A. F. Tedeev, “A Fujita type result for degenerate Neumann problem in domains with noncompact boundary,” J. Math. Anal. Appl., 231, 543–567 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  8. K. Hayakawa, “On nonexistence of global solutions of some semilinear parabolic differential equations,” Proc. Jpn. Acad., Ser. A, Math. Sci., 49, 503–505 (1973).

    Article  MathSciNet  MATH  Google Scholar 

  9. H. A. Levine, “The role of critical exponents in blow up theorems,” SIAM Rev., 32, 262–288 (1990).

    Article  MathSciNet  MATH  Google Scholar 

  10. K. Deng and H. A. Levine, “The role of critical exponents in blow up theorems: The sequel,” J. Math. Anal. Appl., 243, 85–126 (2000).

    Article  MathSciNet  MATH  Google Scholar 

  11. S. Kamin and P. Rosenau, “Nonlinear diffusion in a finite mass medium,” Comm. Pure Appl. Math., 35, 113–127 (1982).

    Article  MathSciNet  MATH  Google Scholar 

  12. S. Kamin and P. Rosenau, “Propagation of thermal waves in an inhomogeneous medium,” Comm. Pure Appl. Math., 34, 831–852 (1981).

    Article  MathSciNet  MATH  Google Scholar 

  13. S. Kamin and R. Kersner, “Disappearance of interfaces in finite time,” Meccanica, 28, 117–120 (1993).

    Article  MATH  Google Scholar 

  14. M. Guedda, D. Hilhorst, and M. A. Peletier, “Disappearing interfaces in nonlinear diffusion,” Adv. Math. Sci. Appl., 7, 695–710 (1997).

    MathSciNet  MATH  Google Scholar 

  15. V. A. Galaktionov and J. R. King, “On the behavior of blow-up interfaces for an inhomogeneous filtration equation,” J. Appl. Math., 57, 53–77 (1996).

    MathSciNet  MATH  Google Scholar 

  16. R. Kersner, G. Reyes, and A. Tesei, “On a class of nonlinear parabolic equations with variable density and absorption,” Adv. Different. Equat., 7, No. 2, 155–176 (2002).

    MathSciNet  MATH  Google Scholar 

  17. V. A. Galaktionov, S. Kamin, R. Kersner, and J. L. Vazquez, “Intermediate asymptotics for inhomogeneous nonlinear heat conduction,” J. Math. Sci., 120, No. 3, 1277–1294 (2004).

    Article  MathSciNet  Google Scholar 

  18. A. F. Tedeev, “Conditions for the existence and nonexistence of the global (in time) compact support of solutions to the Cauchy problem for quasilinear degenerating parabolic equations,” Sib. Mat. Zh., 45, No. 1, 189–200 (2004).

    Article  MathSciNet  MATH  Google Scholar 

  19. A. F. Tedeev, “The interface blow-up phenomenon and local estimates for doubly degenerate parabolic equations,” Appl. Anal., 86, No. 6, 755–782 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  20. Y. W. Qi, “The critical exponents of parabolic equations and blow-up in \( {{\mathbb{R}}^n} \),” Proc. Roy. Soc. Edinburgh A, 128, 123–136 (1998).

    Article  MATH  Google Scholar 

  21. Y. W. Qi and M. X. Wang, “Critical exponents of quasilinear parabolic equations,” J. Math. Anal. Appl., 267, 264–280 (2002).

    Article  MathSciNet  MATH  Google Scholar 

  22. X. Liu and M. Wang, “The critical exponent of doubly singular parabolic equations,” J. Math. Anal. Appl., 257, 170–188 (2001).

    Article  MathSciNet  MATH  Google Scholar 

  23. D. Andreucci and A. F. Tedeev, “Universal bounds at the blow-up time for nonlinear parabolic equations,” Adv. Different. Equat., 10, No. 1, 89–120 (2005).

    MathSciNet  MATH  Google Scholar 

  24. A. V. Martynenko and A. F. Tedeev, “Cauchy problem for the quasilinear parabolic equation with source and inhomogeneous density,” Zh. Vychisl. Mat. Mat. Fiz., 47, No. 2, 245–255 (2007).

    MathSciNet  MATH  Google Scholar 

  25. P. Cianci, A. V. Martynenko, and A. F. Tedeev, “The blow-up phenomenon for degenerate parabolic equations with variable coefficient and nonlinear source,” Nonlin. Anal.: Theory, Meth. Appl., 73, No. 7, 2310–2323 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  26. A. V. Martynenko and A. F. Tedeev, “On the behavior of solutions of the Cauchy problem for the degenerating parabolic equation with inhomogeneous density and source,” Zh. Vychisl. Mat. Mat. Fiz., 48, No. 7, 1214–1229 (2008).

    MathSciNet  Google Scholar 

  27. C. Wang and S. Zheng, “Critical Fujita exponents of degenerate and singular parabolic equations coefficient and nonlinear source,” Proc. Roy. Soc. Edinburgh, A, 136, 415–430 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  28. K. Mukai, K. Mochuzuki, and Q. Huang, “Large time behavior and life span for a quasilinear parabolic equation with slow decay initial values,” Nonlin. Anal., 39A, No. 1, 33–45 (2000).

    Article  Google Scholar 

  29. A. V. Martynenko, A. F. Tedeev, and V. N. Shramenko, “Cauchy problem for the degenerating parabolic equation with inhomogeneous density and source in the class of initial functions slowly approaching zero,” Izv. Ros. Akad. Nauk, Ser. Mat., 76, No. 3, 139–156 (2012).

    MathSciNet  Google Scholar 

  30. N. V. Afanas’eva and A. F. Tedeev, “Fujita-type theorems for quasilinear parabolic equations in the case of slowly vanishing initial data,” Mat. Sb., 195, No. 4, 3–22 (2004).

    Article  MathSciNet  Google Scholar 

  31. D. Andreucci, “Degenerate parabolic equations with initial data measures,” Trans. Amer. Math. Soc., 340, No. 10, 3911–3923 (1997).

    Article  MathSciNet  Google Scholar 

  32. F. Bernis, “Existence results for doubly nonlinear higher order parabolic equations on unbounded domains,” Math. Ann., 279, 373–394 (1988).

    Article  MathSciNet  MATH  Google Scholar 

  33. H. W. Alt and S. Luckhaus, “Quasilinear elliptic-parabolic differential equations,” Math. Z., 183, 311–341 (1983).

    Article  MathSciNet  MATH  Google Scholar 

  34. A. V. Martynenko and A. F. Tedeev, “Regularity of solutions of degenerating parabolic equations with inhomogeneous density,” Ukr. Mat. Vestn., 5, No. 1, 116–145 (2008).

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shevchenko Lugansk National University, Lugansk, Ukraine

    A. V. Martynenko

  2. Institute of Applied Mathematics and Mechanics, Ukrainian National Academy of Sciences, Donetsk, Ukraine

    A. F. Tedeev

  3. “Kiev Polytechnic Institute” National Technical University, Kiev, Ukraine

    V. N. Shramenko

Authors
  1. A. V. Martynenko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. F. Tedeev
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. N. Shramenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 64, No. 11, pp. 1500–1515, November, 2012.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Martynenko, A.V., Tedeev, A.F. & Shramenko, V.N. On the behavior of solutions of the Cauchy problem for a degenerate parabolic equation with source in the case where the initial function slowly vanishes. Ukr Math J 64, 1698–1715 (2013). https://doi.org/10.1007/s11253-013-0745-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11253-013-0745-2

Keywords

Search

Navigation