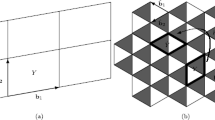
We consider a discrete network of a large number of infinitely thin homogeneous rods oriented along a given vector and connected by elastic springs at each point. The asymptotic behavior of small oscillations of this discrete system is studied in the case where the distances between the nearest rods tend to zero. For general nonperiodic arrays of rods, we deduce equations aimed at the description of the homogenized model of the system. It is shown that the homogenized equations correspond to the asymmetric dynamics of the elastic medium. Indeed, in this case, the stress tensor of the medium linearly depends not only on the strain tensor but also on the rotation tensor.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
E. Cosserat and F. Cosserat, Théorie des Corps Deformables, Hermann, Paris (1909).
G. Grioli, “Ellasticá asymmetrica,” Ann. Mat. Pura Appl., 4, 389–418 (1960).
R. D. Mindlin and H. F. Tiersten, “Effects of couple-stresses in linear elasticity,” Arch. Rat. Mech. Anal., 11, 415–448 (1962).
I. Y. Smolin, P. V. Makarov, D. V. Shmick, and I. V. Savlevich, “A micropolar model of plastic deformation of polycrystals at the mesolevel,” Comp. Mat. Sci., 19, 133–142 (2000).
X. Zhang and P. Sharma, “Inclusions and inhomogeneities in strain gradient elasticity with couple stresses and related problems,” Int. J. Solids Struct., 42, 3833–3851 (2005).
A. I. Leonov, “Algebraic theory of linear viscoelastic nematodynamics,” Math. Phys., Anal. Geom., 11, 87–116 (2008).
M. Berezhnyi and E. Khruslov, “Nonstandard dynamics of elastic composites,” Networks Heterogen. Media, 6, 89–109 (2011).
L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics. Quantum Mechanics. Nonrelativistic Theory, Pergamon Press, London (1958).
G. Friesecke and F. Theil, “Validity and failure of the Cauchy–Born rule in 2D mass-spring lattice,” J. Nonlin. Sci., No. 12, 445–478 (2002).
V. Marchenko and E. Khruslov, Homogenization of Partial Differential Equations, Birkhäuser, Boston (2006).
M. A. Berezhnyy and L. V. Berlyand, “Continuum limit for three-dimensional mass-spring networks and discrete Korn’s inequality,” J. Mech. Phys. Solids, 54, 635–669 (2006).
O. A. Oleinik, A. S. Shamaev, and G. A. Iosif’yan, Mathematical Problems in Elasticity and Homogenization, North-Holland, Amsterdam (1982).
S. Mizohata, The Theory of Partial Differential Equations, Cambridge Univ. Press, New York (1973).
A. M. Kosevich, Theory of Crystal Lattice (Physical Mechanics of Crystals) [in Russian], Vyshcha Shkola, Kharkov (1988).
M. A. Berezhnyi, “The asymptotic behavior of viscous incompressible fluid small oscillations with solid interacting particles,” J. Math. Phys., Anal., Geom., 3, 135–156 (2007).
M. Berezhnyi, L. Berlyand, and E. Khruslov, “The homogenized model of small oscillations of complex fluids,” Networks Heterogen. Media, 3, 835–869 (2008).
M. A. Berezhnyi, Averaged Models of Structurized Liquids [in Ukrainian], Candidate-Degree Thesis (Physics and Mathematics), Kharkiv (2009). URL: http://www.lib.ua-ru.net/diss/cont/354154.html.
A. I. Markushevich, Theory of Analytic Functions [in Russian], Nauka, Moscow (1968).
T. Kato, Perturbation Theory for Linear Operators, Springer, Berlin (1995).
V. A. Ditkin and A. P. Prudnikov, Integral Transforms and Operational Calculus, Pergamon Press, New York (1965).
L. Berlyand and E. Khruslov, “Homogenized non-Newtonian viscoelastic rheology of a suspension of interacting particles in a viscous Newtonian fluid,” SIAM J. Appl. Math., 64, 1002–1034 (2004).
Author information
Authors and Affiliations
Additional information
Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 63, No. 6, pp. 764–785, June, 2011.
Rights and permissions
About this article
Cite this article
Berezhnoi, M.A. Discrete model of the nonsymmetric theory of elasticity. Ukr Math J 63, 891–913 (2011). https://doi.org/10.1007/s11253-011-0551-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-011-0551-7