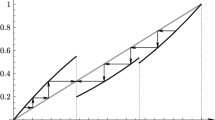
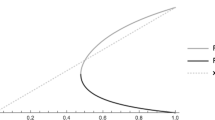
We introduce the notion of Volterra quadratic stochastic operators of a two-sex population. The description of the fixed points of Volterra quadratic stochastic operators of a two-sex population is reduced to the description of the fixed points of Volterra-type operators. Several Lyapunov functions are constructed for the Volterra quadratic stochastic operators of a two-sex population. By using these functions, we obtain an upper bound for the ω-limit set of trajectories. It is shown that the set of all Volterra quadratic stochastic operators of a two-sex population is a convex compact set, and the extreme points of this set are found. Volterra quadratic stochastic operators of a two-sex population that have a 2-periodic orbit (trajectory) are constructed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. N. Bernstein, “Solution of one mathematical problem related to the theory of inheritance,” Uch. Zap. Nauchn.-Issled. Kaf. Ukr. Otd. Mat., 1, 83–115 (1924).
R. N. Ganikhodzhaev, “Quadratic stochastic operators, Lyapunov function, and tournaments,” Mat. Sb., 83, No. 8, 119–140 (1992).
R. N. Ganikhodzhaev, “Map of fixed points and Lyapunov function for one class of discrete dynamical systems,“ Mat. Zametki, 56, 1125–1131 (1994).
R. N. Ganikhodzhaev and D. B. Éshmamatova, “Quadratic automorphisms of a simplex and the asymptotic behavior of trajectories,” Vladikavkaz. Mat. Zh., 8, 12–28 (2006).
R. N. Ganikhodzhaev and M. Kh. Saburov, “Generalized model of nonlinear operators of the Volterra type and Lyapunov function,” J. Sib. Fed. Univ. Math. Phys., 2, 188–196 (2008).
Yu. I. Lyubich, Mathematical Structures in Population Genetics, Springer (1992).
U. A. Rozikov and N. B. Shamsiddinov, “On non-Volterra quadratic stochastic operators generated by a product measure,” Stochast. Anal. Appl., 27, No. 2, 353–362 (2009).
U. A. Rozikov and U. U. Zhamilov, “F -quadratic stochastic operators,” Mat. Zametki, 83, No. 4, 606–612 (2008).
U. A. Rozikov and U. U. Zhamilov, “On the dynamics of strictly non-Volterra quadratic stochastic operators on a two-dimensional simplex,” Mat. Sb., 200, No. 9, 81–94 (2009).
U. A. Rozikov and A. Zada, “On ℓ-Volterra quadratic stochastic operators,” Dokl. Mat., 79, No. 1, 32–34 (2009).
U. U. Zhamilov, “Regularity of F -quadratic stochastic operators,” Uzb. Mat. Zh., No. 2, 35–45 (2008).
U. U. Zhamilov and R. T. Mukhitdinov, “Conditional quadratic stochastic operators,” Uzb. Mat. Zh., No. 2, 31–38 (2010).
G. H. Hardy, J. E. Littlewood, and G. Pólya, Inequalities, Cambridge University, Cambridge (1934).
Author information
Authors and Affiliations
Additional information
Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 63, No. 7, pp. 985–998, July, 2011.
Rights and permissions
About this article
Cite this article
Rozikov, U.A., Zhamilov, U.U. Volterra quadratic stochastic operators of a two-sex population. Ukr Math J 63, 1136–1153 (2011). https://doi.org/10.1007/s11253-011-0568-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-011-0568-y