Hausdorff–Besicovitch dimension of the graph of one continuous nowhere-differentiable function

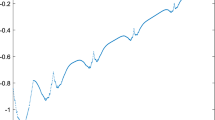
We investigate fractal properties of the graph of the function

$$y = f(x) = \sum\limits_{k - 1}^\infty \frac{{\beta _k }}{{2_k }} \equiv \Delta _{\beta _1 \beta _2 \ldots \beta _{k \ldots } }^2 ,$$

where

$$\beta _1 = \left\{ {\begin{array}{lll} 0 & {{\text{if}}} & {{{\alpha }}_{\text{1}} \left( x \right) = 0,} \\ 1 & {{\text{if}}} & {{{\alpha }}_1 \left( x \right) \ne 0,} \\ \end{array} } \right.$$

$$\beta _k = \left\{ {\begin{array}{lllc} {\beta _{k - 1} } \hfill & {{\text{if}}} \hfill & {\alpha _k \left( x \right) = \alpha _{k - 1} \left( x \right),} \hfill & {} \hfill \\ {1 - \beta _{k - 1} } \hfill & {{\text{if}}} \hfill & {\alpha _k \left( x \right) \ne \alpha _{k - 1} \left( x \right),} \hfill & {k > 1,} \hfill \\ \end{array} } \right.$$

and ‎α _k (x)is the kth ternary digit of x: In particular, we prove that this graph is a fractal set with Hausdorff–Besicovitch α ₀(Г _f )=log₂(1+2^{log 2}₃ ) dimension and cell dimension α^K(Г _f )=2-log₃2.