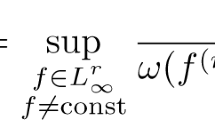Abstract
We obtain new unimprovable Kolmogorov-type inequalities for differentiable periodic functions. In particular, we prove that, for r = 2, k = 1 or r = 3, k = 1, 2 and arbitrary q, p ∈ [1, ∞], the following unimprovable inequality holds for functions \(x \in L_\infty ^r \):
where \(\alpha = \min \left\{ {1 - \frac{k}{r},\frac{{r - k + {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-\nulldelimiterspace} q}}}{{r + {1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-\nulldelimiterspace} p}}}} \right\}\) and ϕ r is the perfect Euler spline of order r.
Similar content being viewed by others
REFERENCES
V. N. Gabushin, “Inequalities for the norms of a function and its derivatives in the metrics of L p,” Mat. Zametki, 1, No. 1, 291–298 (1967).
B. E. Klots, “Approximation of differentiable functions by functions of higher smoothness,” Mat. Zametki, 21, No. 1, 21–32 (1977).
V. M. Tikhomirov and G. G. Magaril-Il'yaev, “Inequalities for derivatives,” in: A. N. Kolmogorov, Selected Works. Mathematics and Mechanics [in Russian], Nauka, Moscow (1985), pp. 387–390.
M. K. Kwong and A. Zettl, “Norm inequalities for derivatives and differences,” Lect. Notes Math., 1536 (1992).
V. V. Arestov and V. N. Gabushin, “The best approximation of unbounded operators by bounded operators,” Izv. Vyssh. Uchebn. Zaved., Ser. Mat., No. 11, 44–66 (1995).
V. F. Babenko, V. A. Kofanov, and S. A. Pichugov, “Inequalities for norms of intermediate derivatives of periodic functions and their applications,” East. J. Approxim., 3, No. 3, 351–376 (1997).
V. F. Babenko, V. A. Kofanov, and S. A. Pichugov, “Inequalities of Landau-Kolmogorov-Nagy type,” in: Abstracts of the International Congress of Mathematicians (Berlin, August 18–27, 1998), Berlin (1998), pp. 115–116.
V. F. Babenko, V. A. Kofanov, and S. A. Pichugov, “ On exact inequalities of Kolmogorov type in the case of low smoothness,” Dopov. Akad. Nauk Ukr, No. 6, 11–14 (1998).
V. N. Gabushin, “On some inequalities for derivatives of functions,” in: V. K. Ivanov (editor), Methods for Regularization of Unstable Problems [in Russian], Institute of Mathematics and Mechanics, Ural Scientific Center, Academy of Sciences of the USSR (1976), pp. 20–26.
N. P. Korneichuk, Exact Constants in Approximation Theory [in Russian], Nauka, Moscow (1987).
A. A. Ligun, “On inequalities for norms of derivatives of periodic functions,” Mat. Zametki, 33, No. 3, 385–391 (1983).
V. F. Babenko, V. A. Kofanov, and S. A. Pichugov, “On exact inequalities of Kolmogorov type that take into account the number of changes in sign of derivatives,” Dopov. Akad. Nauk Ukr., No. 8, 12–16 (1998).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Babenko, V.F., Kofanov, V.A. & Pichugov, S.A. Exact Kolmogorov-Type Inequalities with Bounded Leading Derivative in the Case of Low Smoothness. Ukrainian Mathematical Journal 53, 1569–1582 (2001). https://doi.org/10.1023/A:1015226223806
Issue Date:
DOI: https://doi.org/10.1023/A:1015226223806