Skip to main content
Springer Nature Link
Log in

Homogenization of a Singularly Perturbed Parabolic Problem in a Thick Periodic Junction of the Type 3:2:1

  • Published:
Ukrainian Mathematical Journal Aims and scope

Abstract

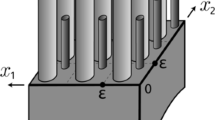
We prove a convergence theorem and obtain asymptotic (as ε → 0) estimates for a solution of a parabolic initial boundary-value problem in a junction Ωε that consists of a domain Ω0 and a large number N 2 of ε-periodically located thin cylinders whose thickness is of order ε = O(N −1).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. V. A. Marchenko and E. Ya. Khruslov, Boundary-Value Problems in Domains with Fine-Grained Boundary [in Russian], Naukova Dumka, Kiev (1974).

    Google Scholar 

  2. A. Bensoussan, J. Lions, and G. Papanicolau, Asymptotic Analysis for Periodic Structure, North Nolland, Amsterdam (1978).

    Google Scholar 

  3. E. Sanchez-Palencia, Nonhomogeneous Media and Vibration Theory, Springer, Berlin (1980).

    Google Scholar 

  4. N. S. Bakhvalov and G. P. Panasenko, Homogenization of Processes in Periodic Media [in Russian], Nauka, Moscow (1984).

    Google Scholar 

  5. O. A. Oleinik, G. A. Iosif'yan, and A. S. Shamaev, Mathematical Problems of the Theory of Strongly Inhomogeneous Elastic Media [in Russian], Moscow University, Moscow (1990).

    Google Scholar 

  6. I. V. Skrypnik, Methods for Investigation on Nonlinear Elliptic Boundary-Value Problems [in Russian], Nauka, Moscow (1990).

    Google Scholar 

  7. V.V. Zhikov, S. M. Kozlov, and O. A. Oleinik, Averaging of Differential Operators [in Russian], Fizmatlit, Moscow (1993).

    Google Scholar 

  8. J. Sanchez-Hubert and E. Sanches-Palencia, Vibration and Coupling of Continuous Systems, Springer, Berlin (1989).

    Google Scholar 

  9. T. A. Mel'nik, “Homogenization of the Poisson equation in a thick periodic junction,” Z.Analysis ihre Anwendungen, 18, No.4, 953–975 (1999).

    Google Scholar 

  10. T. A. Mel'nik and S. A. Nazarov, “Asymptotics of a solution of the spectral Neumann problem in a domain of the ‘thick comb’ type,” Tr.Sem.Petrovsk., 19, 138–174 (1996).

    Google Scholar 

  11. T. A. Mel'nik, “Asymptotic analysis of a spectral problem in a periodic thick junction of type 3:2:1,” Math.Meth.Appl.Sci., 23, No.4, 341–346 (2000).

    Google Scholar 

  12. G. V. Suzikov and E. Ya. Khruslov, “On propagation of sound waves through thin channels in a reflecting layer,” Teor.Funkts.Funkts.Anal.Prilozh., 5, 35–49 (1976).

    Google Scholar 

  13. V. P. Kotlyarov and E. Ya. Khruslov, “On a limit boundary condition for a Neumann problem,” Teor.Funkts.Funkts.Anal.Prilozh., 10, 83–96 (1970).

    Google Scholar 

  14. O. A. Ladyzhenskaya, Boundary-Value Problems in Mathematical Physics [in Russian], Nauka, Moscow (1973).

    Google Scholar 

  15. V. P. Mikhailov, Partial Differential Equations [in Russian], Nauka, Moscow (1983).

    Google Scholar 

  16. S. A. Nazarov, “Junctions of domains of different limit dimensions with singular degeneration,” Tr.Sem.Petrovsk., 18, 1–78 (1995).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Kiev University, Kiev

    T. A. Mel'nik

Authors
  1. T. A. Mel'nik
    View author publications

    You can also search for this author inPubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mel'nik, T.A. Homogenization of a Singularly Perturbed Parabolic Problem in a Thick Periodic Junction of the Type 3:2:1. Ukrainian Mathematical Journal 52, 1737–1748 (2000). https://doi.org/10.1023/A:1010483205109

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1010483205109

Keywords