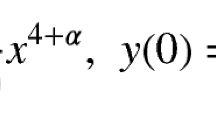Abstract
For functionsf(x) representable by an integral operator of a special form, we investigate the behavior of the second difference Δ 2 h f(x)=f(x+h)-2f(x)+f(x-h),h>0, depending on the location of a pointx on the segment [0,1].
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. F. Timan,Theory of Approximation of Functions of a Real Variable [in Russian], Fizmatgiz, Moscow (1960).
Additional information
Dnepropetrovsk University, Dnepropetrovsk. Translated from Ukrainskii Matematischeskii Zhurnal, Vol. 51, No. 5, pp. 603–613, May, 1999.
Rights and permissions
About this article
Cite this article
Motornyi, V.P. Approximation of fractional-order integrals by algebraic polynomials. I. Ukr Math J 51, 672–683 (1999). https://doi.org/10.1007/BF02591704
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02591704