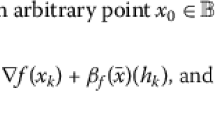Skip to main content
SpringerLink
Log in

Basic properties of the problem of the best simultaneous approximation of several elements

  • Published:
Ukrainian Mathematical Journal Aims and scope

Abstract

For the problem of the best approximation of several elements with respect to the maximum of convex-concave fractional functions with additional restrictions, we establish duality relations and criteria for the element of the best approximation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. N. P. Komeichuk,Extremal Problems in the Theory of Approximation [in Russian], Nauka, Moscow (1976).

    Google Scholar 

  2. V. M. Tikhomirov,Some Problems in the Theory of Approximation [in Russian], Moscow University, Moscow (1976).

    Google Scholar 

  3. P.-J. Laurent,Approximation et Optimisation [Russian translation], Mir, Moscow (1975).

    Google Scholar 

  4. L. Collatz and W. Krabs,Approximationstheorie. Tschebyscheffsche Approximation mit Anwendungen, B. G. Teubner, Stuttgart (1973).

    MATH  Google Scholar 

  5. B. N. Pshenichnyi,Necessary Conditions of Extrenum [in Russian], Nauka, Moscow (1982).

    Google Scholar 

  6. V. O. Gnatyuk, V. V. Moiko, and Yu. V. Gnatyuk, “Basic properties of the problem of best approximation with respect to a fractional function,”Vestn. Kiev. Univ. Fiz.-Mat., Issue 2, 26–31 (1991).

    Google Scholar 

  7. A. D. Ioffe and V. M. Tikhomirov,Theory of Extremal Problems [in Russian], Nauka, Moscow (1974).

    Google Scholar 

Download references

Authors
  1. Yu. V. Gnatyuk
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Kamenets-Podol'skii Pedagogical Institute, Kamenets-Podol'sk. Translated from Ukrainskii Matematicheskii Zhurnal, Vol. 48, No. 9, pp. 1183–1193, September, 1996.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gnatyuk, Y.V. Basic properties of the problem of the best simultaneous approximation of several elements. Ukr Math J 48, 1341–1352 (1996). https://doi.org/10.1007/BF02595356

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02595356

Keywords

Search

Navigation