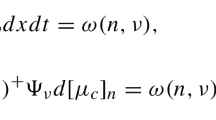Abstract
For divergent elliptic equations with the natural energetic spaceW mp (Ω),m≥1,p>2, we prove that the Dirichlet problem is solvable in a broad class of domains with noncompact boundaries if the growth of the right-hand side of the equation is determined by the corresponding theorem of Phragmén-Lindelöf type. For the corresponding parabolic equation, we prove that the Cauchy problem is solvable for the limiting growth of the initial function % MathType!MTEF!2!1!+-
Similar content being viewed by others
References
V. M. Miklyukov, “On asymptotic properties of subsolutions of quasilinear equations of elliptic type and mappings with limited distortion,”Mat. Sb.,111, No. 1, 42–66 (1980).
A. E. Shishkov, “Behavior of solutions of the Dirichlet problem for quasilinear divergent elliptic equations of higher order in unbounded domains,”Sib. Mat. Zh.,28, No. 6, 134–146 (1987).
O. A. Ladyzhenskaya and V. A. Solonnikov, “On the solution of boundary-value problems for stationary Stokes and Navier-Stokes equations with unbounded Dirichlet integral,”Zap. Nauch. Sem. Leningr. Otd. Mat. Inst. Akad. Nauk SSSR,96, 117–160 (1980).
V. Kalantarov, “On the solution of the first boundary-value problem for the system of von Kárman equations with unbounded energy integral,”Zap. Nauch. Sem. Leningr. Otd. Mat. Inst. Akad. Nauk SSSR,96 (1980).
J.-L. Lions,Some Methods for Solving Nonlinear Boundary-Value Problems [Russian translation], Mir, Moscow (1972).
Yu. A. Dubinskii, “Nonlinear elliptic and parabolic equations,” in:VINITI Series on Contemporary Problems in Mathematics [in Russian], Vol. 9, VINITI, Moscow (1976), pp. 5–130.
A. S. Kalashnikov, “On the Cauchy problem for quasilinear degenerating second-order parabolic equations in classes of growing functions,”Differents. Uravn.,9, No. 4, 682–691 (1973).
A. S. Kalashnikov, “On conditions of uniqueness of generalized solutions of the Cauchy problem for a class of quasilinear degenerating parabolic equations,”Differents. Uravn.,9, No. 12, 2207–2212 (1973).
E. Di Benedetto and M. A. Herrero, “On the Cauchy problem and initial traces for degenerate parabolic equations,”Trans. Amer. Math. Soc. 314, No. 1, 187–224 (1989).
V. F. Akwov and A. E. Shishkov, “On asymptotic properties of solutions of mixed problems for quasilinear parabolic equations in unbounded domains,”Mat. Sb.,182, No. 8, 1200–1210 (1991).
E. Gagliardo, “Ulterori proprieta di ancune classi di funzioni in piu variable,”Ric. Mat.,8, 24–51 (1959).
V. G. Maz'ya,Sobolev Spaces [in Russian], Leningrad University, Leningrad (1985).
F. Bernis, “Finite speed of propagation and asymptotic rates for some nonlinear higher order parabolic equations with absorption,”Proc. Roy. Soc. Edinburgh A,104, 1–19 (1986).
Author information
Authors and Affiliations
Additional information
Translated from Ukrainskii Matematicheskii Zhurnal, Vol. 47, No. 2, pp. 277–289, February, 1995.
Rights and permissions
About this article
Cite this article
Shishkov, A.E. Solvability of boundary-value problems for quasilinear elliptic and parabolic equations in unbounded domains in classes of functions growing at infinity. Ukr Math J 47, 326–340 (1995). https://doi.org/10.1007/BF01056723
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01056723