Abstract
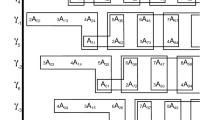
On a three-sheeted Riemannian surfaceR of genus ρ given by an irreducible algebraic equation, we construct normal bases of the ideal of algebraic functions that are multiples of some integer divisors. A method for constructing such normal bases was given in [V. E. Kruglov,Dokl. Akad. Nauk SSSR,321, No. 1, 11–13 (1991)]. The relations obtained for the exponents of the constructed elements enable one to determine the number of solutions of the Riemann problem for any integer divisor and to find partial indices in the problems of factorization of matrices of permutation type.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. E. Kruglov, “On algebraic functions that are multiples of a given divisor,”Dokl. Akad. Nauk SSSR,321, No. 1, 11–13 (1991).
L. N. Kolmakova, “On a singular integral equation with many-valued kernel on a hyperelliptic Riemannian surface,”Ukr. Mat. Zh.,37, No. 5, 630–633 (1985).
E. I. Zverovich and L. I. Pomerantseva, “Riemann problem forn pairs of functions with matrices of permutation type,”Dokl. Akad. Nauk SSSR,217, No. 1, 20–23 (1974).
V. E. Kruglov, “On the number of linearly independent functions that are multiples of a given divisor containing conjugate points of a Riemannian surface of an algebraic function,”Izv. Vyssh. Uchebn. Zaved., Mat., No. 2 (153), 119–122 (1975).
Author information
Authors and Affiliations
Additional information
Translated from Ukrainskii Matematicheskii Zhurnal, Vol. 47, No. 8, pp. 1029–1037, August, 1995.
Rights and permissions
About this article
Cite this article
Kolmakova, L.N. Exponents of elements of a normal basis of the ideal of algebraic functions on a three-sheeted Riemannian surface. Ukr Math J 47, 1178–1187 (1995). https://doi.org/10.1007/BF01057708
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01057708