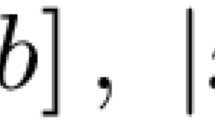Abstract
For each functionf(x) continuous on the segment [−1, 1], we set\(\tilde f(t) = f(\cos t)\). We study the relationship between the ordinarykth modulus of continuity\(\omega _k (\tau ,\tilde f^{(r)} )\) of therth derivative\(\tilde f^{(r)}\) of the function\(\tilde f\) and thekth modulus of continuity\(\bar \omega _{k,r} (\tau ,f^{(r)} )\) with weight ϕ r of the rth derivativef (r) of the functionf introduced by Ditzian and Totik. Thus, ifr is odd andk is even, we prove that these moduli are equivalent ast→0.
Similar content being viewed by others
References
Z. Ditzian and V. Totik,Moduli of Smoothness, Springer, New York, etc. (1987).
L. G. Shakh, “On the equivalence of some definitions ofkth moduli of continuity,” in:Fourier Series. Theory and Applications [in Russian], Institute of Mathematics, Ukrainian Academy of Sciences, Kiev (1992), pp. 154–160.
V. K. Dzyadyk,Introduction to the Theory of Uniform Approximation of Functions by Polynomials [in Russian], Nauka, Moscow (1977).
I. A. Shevchuk,Approximation by Polynomials and Traces of Continuous Functions Defined on Segments [in Russian], Naukova Dumka, Kiev (1992).
Author information
Authors and Affiliations
Additional information
Translated from Ukrainskii Matematicheskii Zhurnal, Vol. 47, No. 12, pp. 1627–1638, December, 1995.
Rights and permissions
About this article
Cite this article
Dyuzhenkova, O.Y. A remark concerning the modulus of smoothness introduced by Ditzian and Totik. Ukr Math J 47, 1858–1872 (1995). https://doi.org/10.1007/BF01060960
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01060960