Skip to main content
SpringerLink
Log in

Potential theory for problems of diffraction on a layer between two parallel planes

  • Published:
Ukrainian Mathematical Journal Aims and scope

Abstract

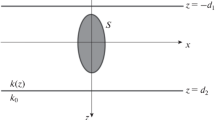
We investigate the boundary-value problems that appear when studying the diffraction of acoustic waves on obstacles in a layer between two parallel planes. By using potential theory, these boundary-value problems are reduced to the Fredholm integral equations given on the boundary of the obstacles. The theorems on existence and uniqueness are proved for the Fredholm equations obtained and, hence, for the boundary-value problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Yu. K. Podlipenko,Potential Theory for Problems of Diffraction in a Wedge and in a Layer [in Russian], Preprint No. 55, Institute of Mathematics, Ukrainian Academy of Sciences, Kiev (1988).

    Google Scholar 

  2. Yu. K. Podlipenko,Boundary-Value Problems for the Heimholtz Equation in Regions with Infinite Boundaries [in Russian], Preprint No. 90.47, Institute of Mathematics, Ukrainian Academy of Sciences, Kiev (1990).

    Google Scholar 

  3. K. Morgenröther and P. Werner, “On the instability of resonances in parallel-plane waveguides,”Math. Methods Appl. Sci.,11, No. 3, 279–315 (1989).

    Google Scholar 

  4. D. S. Jones, “The eigenvalues of ▽2 u + λu=0,”Proc. Cambridge Phil. Soc.,49, No. 4, 668–684 (1953).

    Google Scholar 

  5. A. G. Sveshnikov, “On the radiation principle,”Dokl. Akad. Nauk SSSR,75, No. 5, 917–920 (1950).

    Google Scholar 

  6. A. S. ll'inskii and Yu. V. Shestopalov,Application of the Methods of Spectral Theory to the Problems of Wave Propagation [in Russian], Moscow University, Moscow (1989).

    Google Scholar 

  7. D. Colton and R. Kress,Integral Equation Methods in Scattering Theory [Russian translation], Mir, Moscow (1987).

    Google Scholar 

  8. S. Mizohata, ‘Theory of Partial Differential Equations [Russian translation]. Mir, Moscow (1977).

    Google Scholar 

  9. D. S. Kuznetsov,Special Functions [in Russian], Vysshaya Shkola, Moscow (1965).

    Google Scholar 

  10. H. Bateman and A. Erdélyi,Higher Transcendental Functions, Vol. 2, McGraw-Hill, New York (1954).

    Google Scholar 

  11. M. Abramowitz and I. Stegun (editors),Handbook of Mathematical Functions [Russian translation], Nauka, Moscow (1979).

    Google Scholar 

  12. G. E. Shilov,Integral, Measure, and Derivative [in Russian], Nauka, Moscow (1967).

    Google Scholar 

  13. J. B. Keller and J. S. Papadakis (editors),Wave Propagation and Underwater Acoustics [Russian translation], Mir, Moscow (1980).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Kiev University, Kiev

    Yu. K. Podlipenko

Authors
  1. Yu. K. Podlipenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Ukrainskii Matematicheskii Zhurnal, Vol. 45, No. 5, pp. 647–662, May, 1993.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Podlipenko, Y.K. Potential theory for problems of diffraction on a layer between two parallel planes. Ukr Math J 45, 706–723 (1993). https://doi.org/10.1007/BF01058207

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01058207

Keywords

Search

Navigation